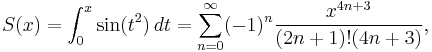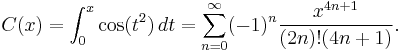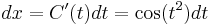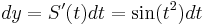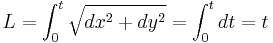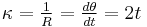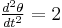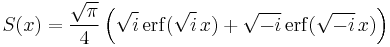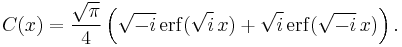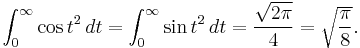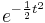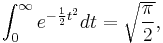Fresnel integral

Fresnel integrals, S(x) and C(x), are two transcendental functions named after Augustin-Jean Fresnel that are used in optics. They arise in the description of near field Fresnel diffraction phenomena, and are defined through the following integral representations:

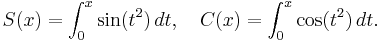
S(x)=\int_0^x \sin(t^2)\,dt,\quad C(x)=\int_0^x \cos(t^2)\,dt.

The simultaneous parametric plot of S(x) and C(x) is the Euler spiral, also known as the Cornu spiral or clothoid.

Contents

Definition

The Fresnel integrals admit the following power series expansions that converge for all x:

S(x)=\int_0^x \sin(t^2)\,dt=\sum_{n=0}^{\infin}(-1)^n\frac{x^{4n%2B3}}{(2n%2B1)!(4n%2B3)},
C(x)=\int_0^x \cos(t^2)\,dt=\sum_{n=0}^{\infin}(-1)^n\frac{x^{4n%2B1}}{(2n)!(4n%2B1)}.

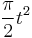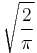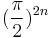Some authors, including Abramowitz and Stegun, (eqs 7.3.1 – 7.3.2) use \frac{\pi}{2}t^2 for the argument of the integrals defining S(x) and C(x). To get these functions, multiply the above integrals by \sqrt{\frac{2}{\pi}} and multiply the argument x by (\frac{\pi}{2})^{2n}.

Euler spiral

Main article: Euler spiral

The Euler spiral, also known as Cornu spiral or clothoid, is the curve generated by a parametric plot of S(t) against C(t). The Cornu spiral was created by Marie Alfred Cornu as a nomogram for diffraction computations in science and engineering.

From the definitions of Fresnel integrals, the infinitesimals dx and dy are thus:

dx = C'(t)dt = \cos(t^2) dt \,
dy = S'(t)dt = \sin(t^2) dt \,

Thus the length of the spiral measured from the origin can be expressed as:

L = \int_0^t {\sqrt {dx^2 %2B dy^2}} = \int_0^t{dt} = t

That is, the parameter t is the curve length measured from the origin (0,0) and the Euler spiral has infinite length. The vector [cos(t²), sin(t²)] also expresses the unit tangent vector along the spiral, giving θ = t². Since t is the curve length, the curvature, \kappa can be expressed as:

\kappa = \tfrac {1}{R} = \tfrac {d\theta}{dt} = 2t

And the rate of change of curvature with respect to the curve length is:

\tfrac {d^2\theta}{dt^2} = 2

An Euler spiral has the property that its curvature at any point is proportional to the distance along the spiral, measured from the origin. This property makes it useful as a transition curve in highway and railway engineering.

If a vehicle follows the spiral at unit speed, the parameter t in the above derivatives also represents the time. That is, a vehicle following the spiral at constant speed will have a constant rate of angular acceleration.

Sections from Euler spirals are commonly incorporated into the shape of roller-coaster loops to make what are known as "clothoid loops".

Properties

S(x)=\frac{\sqrt{\pi}}{4} \left( \sqrt{i}\,\operatorname{erf}(\sqrt{i}\,x) %2B \sqrt{-i}\,\operatorname{erf}(\sqrt{-i}\,x) \right)
C(x)=\frac{\sqrt{\pi}}{4} \left( \sqrt{-i}\,\operatorname{erf}(\sqrt{i}\,x) %2B \sqrt{i}\,\operatorname{erf}(\sqrt{-i}\,x) \right).
\int_{0}^{\infty} \cos t^2\,dt = \int_{0}^{\infty} \sin t^2\,dt = \frac{\sqrt{2\pi}}{4} = \sqrt{\frac{\pi}{8}}.

Evaluation

The limits of C and S as the argument tends to infinity can be found by the methods of complex analysis. This uses the contour integral of the function

e^{-\frac{1}{2}t^2}

around the boundary of the sector-shaped region in the complex plane formed by the positive x-axis, the half-line y = x, x ≥ 0, and the circle of radius R centered at the origin.

As R goes to infinity, the integral along the circular arc tends to 0, the integral along the real axis tends to the Gaussian integral

\int_{0}^{\infty} e^{-\frac{1}{2}t^2}dt = \sqrt{\frac{\pi}{2}},

and after routine transformations, the integral along the bisector of the first quadrant can be related to the limit of the Fresnel integrals.

Generalization

The Fresnel integral can be generalized by the function

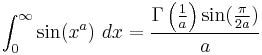
\int_0^\infty\sin(x^a)\ dx = \frac{\Gamma\left(\frac{1}{a}\right)\sin(\frac{\pi}{2a})}{a}

with the left-hand side converging for a>1 and the right-hand side being its analytical extension to the whole plane less where lie the poles of 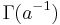\Gamma(a^{-1}).

See also

References

External links